Measuring Sound Intensity
Human ears are remarkably sensitive to vibrations in the air. The threshold of human
hearing is around 20 microPascals (μP), which is an extremely small amount of
atmospheric pressure. At the other extreme, the loudest sound a person can withstand
without pain or ear damage is about 200,000,000 μP: for example, a loud rock concert
or a nearby jet airplane taking off.
Because the human ear can handle such a large range of intensities, measuring sound
pressure levels on a linear scale is inconvenient. For example, if the range of human
hearing were measured on a ruler, the scale would go from 1 foot (quietest) to over
3000 miles (loudest)! To make this huge range of numbers easier to work with, a
logarithmic unit—the decibel—is used. Logarithms map exponential values to a linear
scale. For example, by taking the base-ten logarithm of 10 (10
1
) and 1,000,000,000 (10
9
), this
large range of numbers can be written as 1–9, which is a much more convenient scale.
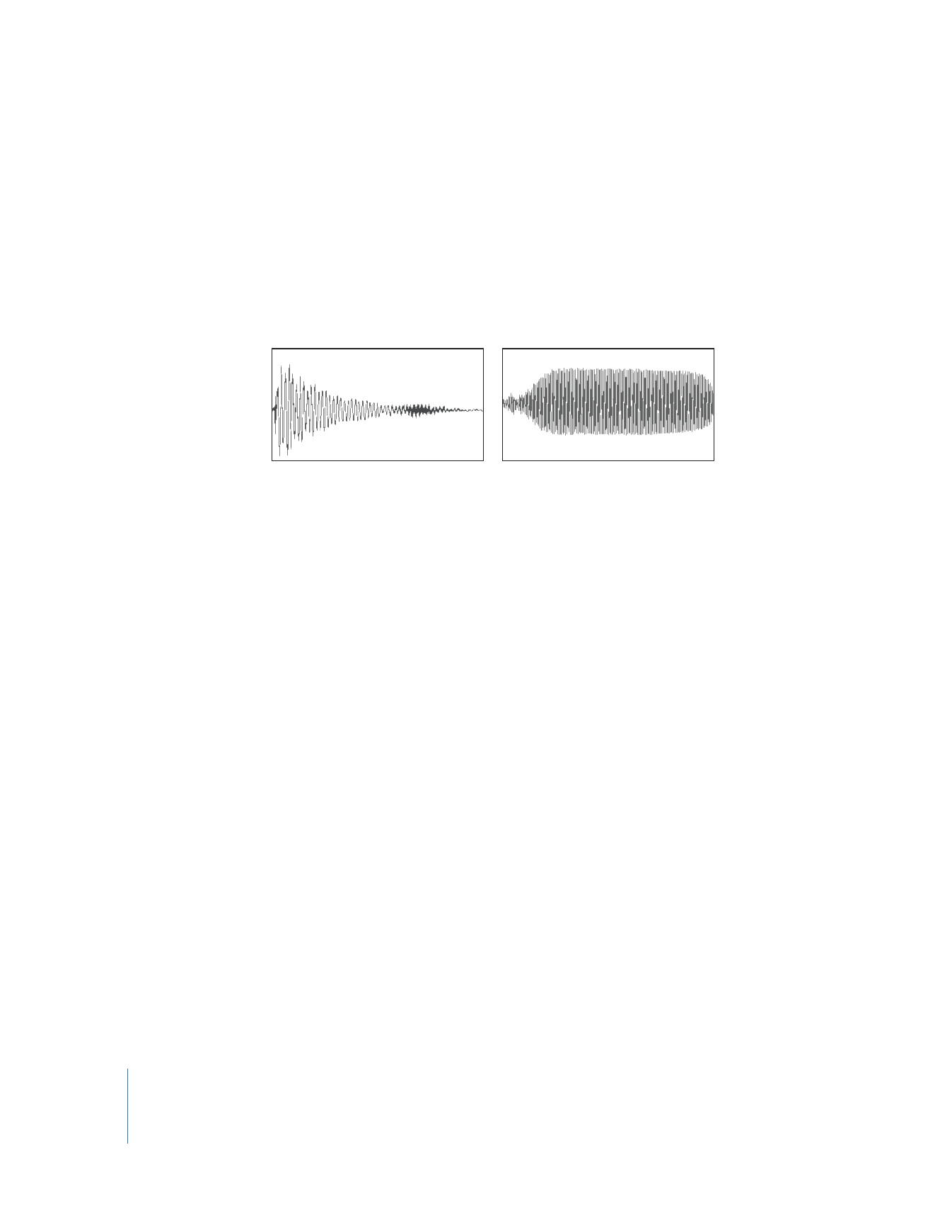
Percussive volume envelope
Sustained volume envelope

Chapter 1
Audio Fundamentals
23
I
Because the ear responds to sound pressure logarithmically, using a logarithmic
scale corresponds to the way humans perceive loudness. Audio meters and sound
measurement equipment are specifically designed to show audio levels in decibels.
Small changes at the bottom of an audio meter may represent large changes in signal
level, while small changes toward the top may represent small changes in signal level.
This makes audio meters very different from linear measuring devices like rulers,
thermometers, and speedometers. Each unit on an audio meter represents an
exponential increase in sound pressure, but a perceived linear increase in loudness.
Important:
When you mix audio, you don’t need to worry about the mathematics
behind logarithms and decibels. Just be aware that to hear incremental increases in
sound volume, exponentially more sound pressure is required.